Volume Word Problems 8th Grade Pdf

I begin today with a review of the difference between area and perimeter. For second grade the CCSS (2.OA.C.4 and 2 GA.2) expects students to be able to create rectangular arrays, to partition of the center and count the squares to find the total, or the area of the figure. Perimeter is not introduced in second grade, but because it is part of the district expectations, I introduce it, and use perimeter as a way to practice the adding of 2- and 3-digit numbers in expanded form. I begin with a review of area. I draw a rectangle on the board and tell students it is 4 blocks long and 2 blocks wide.

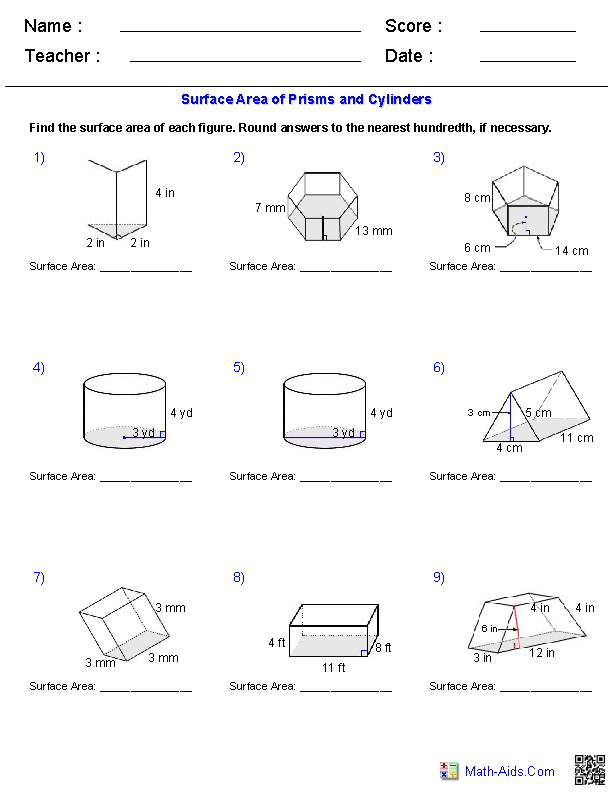
Find volume of rectangular prisms to solve word problems. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

I ask if anyone can come and mark off my shape to find the area. Which is area, the space covered by the rectangle or the distance around its outside? Was it the grass on the farmer's field or the fence around his lettuce? (This is a reference to the introductory lessons on area and perimeter.) After one student has partitioned off the shape and counted the area, I ask the other students for confirmation that this is correct. I repeat this with a second shape beside the first. Now I ask if we could find the perimeter or distance around the outside of the shape?

We look at the word area which is shorter than perimeter just as in is shorter than out, as another way to remember which is which. I ask for volunteers to find the perimeter of each shape. We check to see if the area and perimeter are the same. We find that for these rectangles they are different. I have prepared that has a review of expanded form addition and subtraction, as well as a series of perimeter and area word problems for students to solve. When I do the examples I show students how I make a model of the number by expanding it out.

I can put the numbers back together as well. Contoh soal tap universitas terbuka. Expanded form is an exercise in modeling with mathematics an understanding that a number can be broken apart and put back together again (MP4). I start by putting the following equation on the board: 600 + 20 + 5 + 300 + 40 + 3 = We work together, putting hundreds with hundreds, tens with tens, and ones with ones: 900 + 60 + 8 = 968 I tell students that my second one will be a bit harder.

I write: 200 + 20 + 9 + 200 + 40 + 6 Now when we put hundreds with hundreds, tens with tens, and ones with ones, we get: 400 + 60 + 15 I ask students if we can have 15 in the ones place? So what do we have to do? We have to bring ten of those into the ten's place so now we have: 400 + 60 + 10 + 5 = 400 + 70 + 5 = 475 I repeat this process with several subtraction problems, first with no borrowing and then final 2 examples with borrowing. For example: 481 - 225 = 400 + 80 + 1 - 200 + 20 + 5 I begin by matching the ones and I have 1 - 5, which I can't do so I go to the 80 and break it into 70 + 10 so I have 400 + 70 + 10 + 1.